📚ug Sem 1 Physics Vector Analysis Physics ✍🏻handwrittennotes Degree Vector Ug

Physics At A Glance Vector Analysis For complete pdf access whatsapp on 6302127724. Define relevant terms such as action and reaction, vector components, impulse, elastic and inelastic collisions, etc.
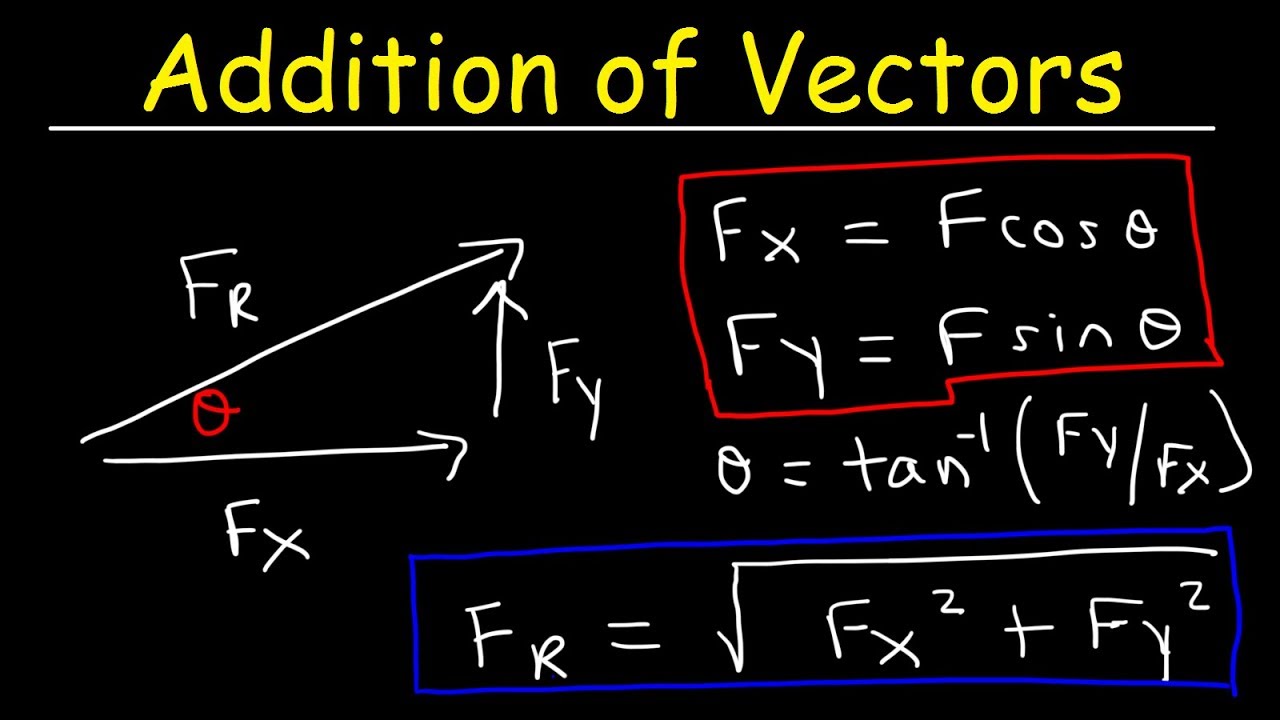
Vector Formula Physics At Vectorified Collection Of Vector Vector analysis bridget lobo physics notes unit 02: vector analysis section 01: scalar vector quantities scalar: can be defined using one numerical quantity. 3 ˆn= 1 2. if ˆn is the unit vector pointing out of the page, it follows that a⇥(b c)=(a⇥b) (a⇥c). (cross product is distributive) (b) for the general case, see g. e. hay’s vector and tensor analysis, chapter 1, section 7 (dot product) and section 8 (cross product) problem 1.2 chapter 1. vector analysis 3 chapter 1 vector analysis. This document discusses vectors and vector addition in physics. it begins by defining scalar and vector quantities, with vectors having both magnitude and direction while scalars only have magnitude. it describes representing vectors with arrows and discussing concepts like equal, parallel, antiparallel vectors. Perform vector algebra in terms of vector components. relate the displacements and velocities of objects viewed in different reference frames using vector diagrams and reference frame transformation relations.

Solution Physics Vector Analysis Studypool This document discusses vectors and vector addition in physics. it begins by defining scalar and vector quantities, with vectors having both magnitude and direction while scalars only have magnitude. it describes representing vectors with arrows and discussing concepts like equal, parallel, antiparallel vectors. Perform vector algebra in terms of vector components. relate the displacements and velocities of objects viewed in different reference frames using vector diagrams and reference frame transformation relations. Position, displacement, velocity, acceleration, force, and momentum are all physical quantities that can be represented mathematically by vectors. the set of vectors and the two operations form what is called a vector space. 1.1.9 vector product (a) definition this product is a vector rather than scalar in character, but it is a vector in a somewhat restricted sense. the vector product of a and b is defined as c a b a b sin nˆ absin nˆ where a is the magnitude of a. b is the magnitude of b. is the angle between a and b. Tpoics covered:historic backgroundcurrent day applicationsdefining the magnitude of vectors.defining the direction of vectors.ppt: drive.google o. Chapter 6: vector analysis we use derivatives and various products of vectors in all areas of physics. for example, newton’s 2nd law is f~= md2~r dt2. in electricity and magnetism, we need surface and volume integrals of various elds. fields can be scalar in some cases, but often they are vector elds like e~(x;y;z) and b~(x;y;z).

Solution Physics Vector Analysis Studypool Position, displacement, velocity, acceleration, force, and momentum are all physical quantities that can be represented mathematically by vectors. the set of vectors and the two operations form what is called a vector space. 1.1.9 vector product (a) definition this product is a vector rather than scalar in character, but it is a vector in a somewhat restricted sense. the vector product of a and b is defined as c a b a b sin nˆ absin nˆ where a is the magnitude of a. b is the magnitude of b. is the angle between a and b. Tpoics covered:historic backgroundcurrent day applicationsdefining the magnitude of vectors.defining the direction of vectors.ppt: drive.google o. Chapter 6: vector analysis we use derivatives and various products of vectors in all areas of physics. for example, newton’s 2nd law is f~= md2~r dt2. in electricity and magnetism, we need surface and volume integrals of various elds. fields can be scalar in some cases, but often they are vector elds like e~(x;y;z) and b~(x;y;z).

Comments are closed.