Vector Fields Divergence And Curl

Solved Curl And Divergence Of A Vector Field Find The Chegg Use the properties of curl and divergence to determine whether a vector field is conservative. in this section, we examine two important operations on a vector field: divergence and curl. In this section we will introduce the concepts of the curl and the divergence of a vector field. we will also give two vector forms of green’s theorem and show how the curl can be used to identify if a three dimensional vector field is conservative field or not.
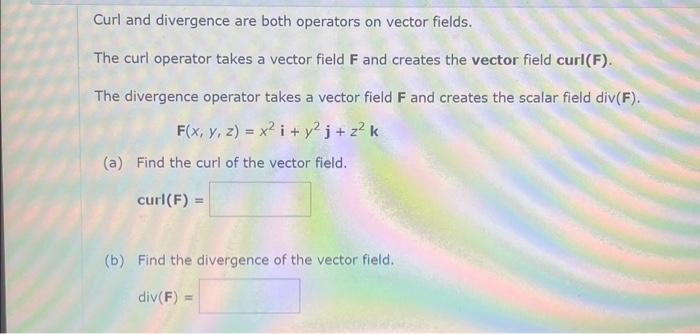
Solved Curl And Divergence Are Both Operators On Vector Chegg Divergence and curl are mathematical operators, divergence is a differential operator, which is applied to the 3d vector valued function. whereas, the curl is a vector operator which defines the infinitesimal circulation of a vector field in the 3d euclidean space. The divergence of a vector field \(\vecs{f} (x,y,z)\) is the scalar valued function \[ \text{div}\,\vecs{f} =\vecs{ \nabla} \cdot\vecs{f} = \frac{\partial f 1}{\partial x} \frac{\partial f 2}{\partial y} \frac{\partial f 3}{\partial z} \nonumber \]. Vector fields, curl and divergence examples of vector elds • thegravitational force elddescribes the force of attraction of the earth on a mass m and is given by f = mmg r3 r; where r := (x;y;z) and r := krk:the vector eld f points to the centre of the earth. • the vector eld f : r2!r2 given by f(x;y) := ( y;x). In vector calculus, the curl, also known as rotor, is a vector operator that describes the infinitesimal circulation of a vector field in three dimensional euclidean space. the curl at a point in the field is represented by a vector whose length and direction denote the magnitude and axis of the maximum circulation. [1] .
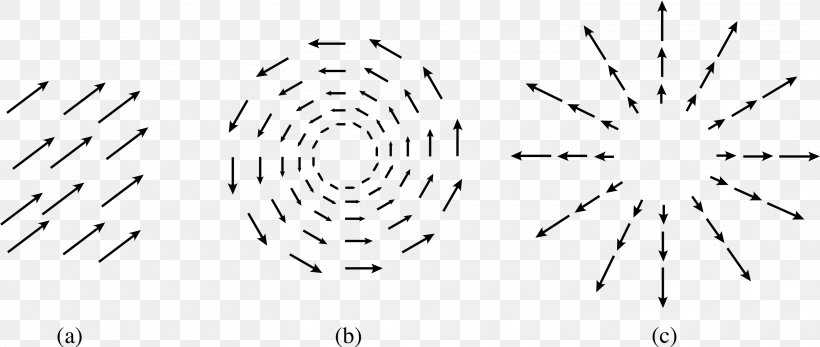
Curl Divergence Vector Field Vector Calculus Png 2920x1237px Vector fields, curl and divergence examples of vector elds • thegravitational force elddescribes the force of attraction of the earth on a mass m and is given by f = mmg r3 r; where r := (x;y;z) and r := krk:the vector eld f points to the centre of the earth. • the vector eld f : r2!r2 given by f(x;y) := ( y;x). In vector calculus, the curl, also known as rotor, is a vector operator that describes the infinitesimal circulation of a vector field in three dimensional euclidean space. the curl at a point in the field is represented by a vector whose length and direction denote the magnitude and axis of the maximum circulation. [1] . This applet allows you to visualize vector fields and their divergence and curl, as well as work done by a field. choose a field from the drop down box. drag the curl paddle and divergence dot around the field to see how these change. select a path to see the work done by the field along the path. Divergence and curl are fundamental concepts in vector calculus, extensively used to study the behavior of vector fields. these operations help describe how a vector field changes or flows through space, giving insights into the nature of the field itself. In two dimensions, the divergence is just the curl of a −90 degrees rotated field g = hq,−pi because div(g) = qx − py = curl(f). the divergence measures the ”expansion” of a field. if a field has zero divergence everywhere, the field is called incompressible. The divergence and curl of a vector field are two vector operators whose basic properties can be understood geometrically by viewing a vector field as the flow of a fluid or gas.

Divergence And Curl Example Math Insight This applet allows you to visualize vector fields and their divergence and curl, as well as work done by a field. choose a field from the drop down box. drag the curl paddle and divergence dot around the field to see how these change. select a path to see the work done by the field along the path. Divergence and curl are fundamental concepts in vector calculus, extensively used to study the behavior of vector fields. these operations help describe how a vector field changes or flows through space, giving insights into the nature of the field itself. In two dimensions, the divergence is just the curl of a −90 degrees rotated field g = hq,−pi because div(g) = qx − py = curl(f). the divergence measures the ”expansion” of a field. if a field has zero divergence everywhere, the field is called incompressible. The divergence and curl of a vector field are two vector operators whose basic properties can be understood geometrically by viewing a vector field as the flow of a fluid or gas.
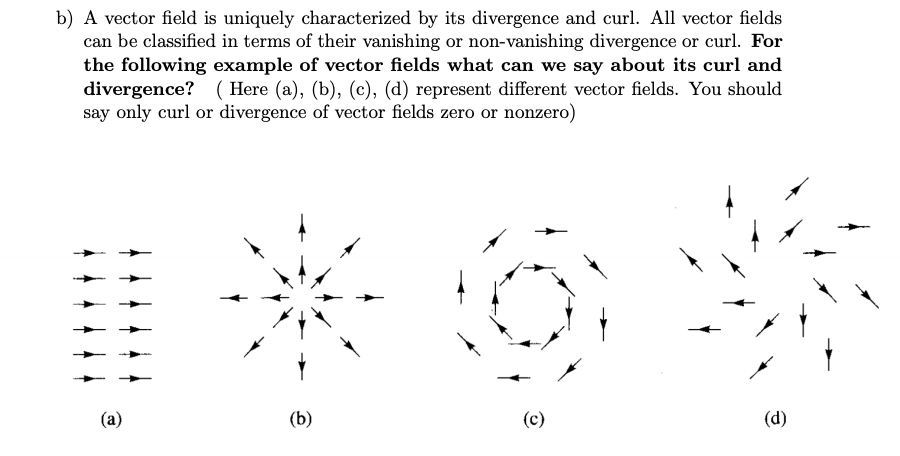
Solved B A Vector Field Is Uniquely Characterized By Its Chegg In two dimensions, the divergence is just the curl of a −90 degrees rotated field g = hq,−pi because div(g) = qx − py = curl(f). the divergence measures the ”expansion” of a field. if a field has zero divergence everywhere, the field is called incompressible. The divergence and curl of a vector field are two vector operators whose basic properties can be understood geometrically by viewing a vector field as the flow of a fluid or gas.

Comments are closed.