Vectors Precalculus

Vectors Making Precalculus Fun Performing operations with vectors in terms of i and j . so far, we have investigated the basics of vectors: magnitude and direction, vector addition and subtraction, scalar multiplication, the components of vectors, and the representation of vectors geometrically. In this section, we will investigate another way to approach the problem using vectors, a geometric entity that indicates both a distance and a direction. we will begin our investigation using a purely geometric view of vectors.

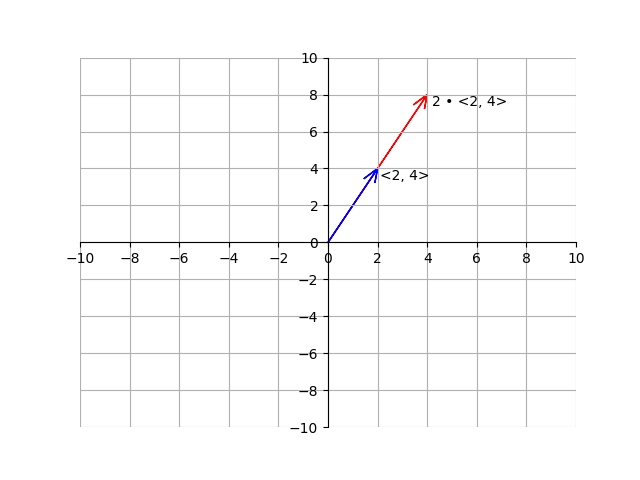
Here Is The Example But Geometrically View vectors geometrically. find magnitude and direction. perform vector addition and scalar multiplication. find the component form of a vector. find the unit vector in the direction of [latex]\boldsymbol{v}[ latex] . perform operations with vectors in terms of [latex]\boldsymbol{i}[ latex] and [latex]\boldsymbol{j}[ latex] . 4.8.a identify characteristics of a vector. 4.8.b determine sums and products involving vectors. *ap® is a trademark registered and owned by the collegeboard, which was not involved in the production of, and does not endorse, this site. In precalculus, vectors are typically introduced as ordered pairs or triples, with each component representing the magnitude in a specific direction. they play a crucial role in solving problems involving motion, forces, and geometry. This section covers vectors from an algebraic perspective, including expressing vectors in coordinate form, math 375: pre calculus 8: non right triangle trigonometry 8.5: vectors an algebraic approach expand collapse global location 8.5: vectors an algebraic approach.

Mastering Vectors In Precalculus A Comprehensive Guide In precalculus, vectors are typically introduced as ordered pairs or triples, with each component representing the magnitude in a specific direction. they play a crucial role in solving problems involving motion, forces, and geometry. This section covers vectors from an algebraic perspective, including expressing vectors in coordinate form, math 375: pre calculus 8: non right triangle trigonometry 8.5: vectors an algebraic approach expand collapse global location 8.5: vectors an algebraic approach. Graph the vectors \(\vec{v}, \vec{w}, \vec{r}, \vec{s}, \vec{t}\) in the plane, where \(\vec{v}=\overrightarrow{pq}\) with \(p(6,3)\) and \(q(4, 2)\), and \[\vec{w}=\langle 3, 1\rangle, \quad \vec{r}=\langle 4, 2\rangle, \quad \vec{s}=\langle 0, 2\rangle, \quad \vec{t}=\langle 5, 3\rangle \nonumber \]. All vectors have two things: direction – follow the arrow. magnitude – the length of the vector. graphing vectors . use the vector to graph each of the following vectors:. Adding vectors by components any vector can be expressed as the sum of two other vectors, which are called its components. usually the other vectors are chosen so that they are perpendicular to each other. resolve vectors into perpendicular components along chosen axes.

Introduction To Vectors Precalculus Introduction Lesson Graph the vectors \(\vec{v}, \vec{w}, \vec{r}, \vec{s}, \vec{t}\) in the plane, where \(\vec{v}=\overrightarrow{pq}\) with \(p(6,3)\) and \(q(4, 2)\), and \[\vec{w}=\langle 3, 1\rangle, \quad \vec{r}=\langle 4, 2\rangle, \quad \vec{s}=\langle 0, 2\rangle, \quad \vec{t}=\langle 5, 3\rangle \nonumber \]. All vectors have two things: direction – follow the arrow. magnitude – the length of the vector. graphing vectors . use the vector to graph each of the following vectors:. Adding vectors by components any vector can be expressed as the sum of two other vectors, which are called its components. usually the other vectors are chosen so that they are perpendicular to each other. resolve vectors into perpendicular components along chosen axes.